WikiSysop
| Line 1: | Line 1: | ||
<hr style='width:80%; height:8px; background-color:teal;'/> | <hr style='width:80%; height:8px; background-color:teal;'/> | ||
{{list_subpages|user|wikisysop|caption=Subpages}} | {{list_subpages|user|wikisysop|caption=Subpages}} | ||
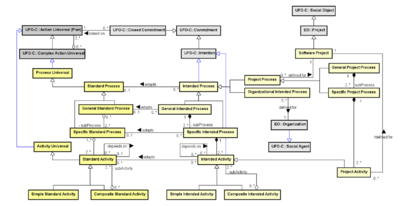
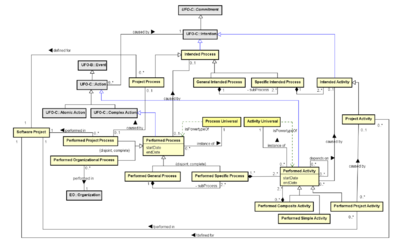
{{/Information Model}} | |||
<hr style='width:80%; height:8px; margin-top:2em; background-color:teal;'/> | |||
<hr style='width:80%; height:8px; background-color:teal;'/> | |||
{{/Tasklist}} | {{/Tasklist}} | ||
<hr style='clear:both;background-color:green'/> | <hr style='clear:both;background-color:green'/> | ||
Revision as of 14:51, 25 November 2022
wikisysop:
The Best Practices Wiki Ontology
The scientific method is a systematic approach to acquiring knowledge and understanding about the natural world. The epistemology that underpins the scientific method is empiricism, which is the idea that knowledge comes from observation and experimentation. This means that scientific knowledge is based on evidence that can be observed, measured, and tested, and that scientific theories and hypotheses must be testable and falsifiable in order to be considered valid. The scientific method is also characterized by the principles of skepticism and critical thinking, which require that scientists question existing beliefs and carefully evaluate new evidence in order to arrive at well-supported conclusions.
An Emergence Epistemology for Modern Ontologies
On the heels of recent evolution in mathematics and astronomy, physics, biology, social sciences, and cognitive research, a new approach to the process of information modeling is needed to support widely common cross-domain requirements, that is, this article proposes a candidate Standard Ontology Model (SOM).
Motivation
Presently ontologies are built using approaches first typified by the Formula Translating System (FORTRAN), and are thus based on essential notions of "data structures" as proxies for operands to an algebraic formula; "routines" being a particular functional formula; and "return values" being the specific knowable output of the formula. The generic formula, y = f(x) (where "y" is equal to "f" upon "x") exactly maps to the widespread Input-Process-Output model underpinning many methods; it is apt to consider this Algebraic Formula an epistemology itself as its method of organization of inputs and outputs (as instances of an equivalence relation) is strictly domain-neutral.
However if success of ontologies is judged by their fruits, the Formula paradigm appears to have produced representations of reality that are not being used to an overwhelming degree, by anyone, for the principle reason the ontologies being promulgated as "common and global and domain-neutral" have no bearing on the models being developed and tested by a data scientist most concerned with theories of interaction and evolution within their chosen domains. The core problem is no public ontology exists to structure the problem-solving space needed by data scientists, thereby reducing use of ontologies to that of a public gesture.
Formula data structures first emerged as Database Systems and then as Triple Stores. Triple Stores consolidated gargantuan systems of DBMS tables, using ontologies as a dictionary of existential relations between keys inherited from those tables, in theory to reduce processing costs while increasing processing opportunities.
The Resource Description Framework (RDF) introduced a model for an Axiom (expressed in any of several RDF Notations) with its rdf:Statement construct, a "triple" composed of three pieces, {rdf:Subject, rdf:Predicate, rdf:Object}, essential to logic processors. RDF also addressed list processors, defining without further comment, the rdf:Pair = {rdf:First, rdf:Rest} construct. The most fundamental RDF concept is rdf:Resource an identifiable but otherwise void concept that is the basis for rdf:Individual to which property values are attached (with each property name defined by an instance of rdf:Property). A categorical "class" is also associated with every Individual when it is instantiated (with each class name defined by an instance of rdfs:Class').
Finally it is noted the Standard Model-View-Controller Model taught to computer science students is a "triple" relation too, catering to a growing orientation towards database models, process models and ontology models.
Review of Prior Art
Ontology Engineering (Wikipedia)
In computer science, information science and systems engineering, ontology engineering is a field which studies the methods and methodologies for building ontologies, which encompasses a representation, formal naming and definition of the categories, properties and relations between the concepts, data and entities. In a broader sense, this field also includes a knowledge construction of the domain using formal ontology representations such as OWL/RDF. A large-scale representation of abstract concepts such as actions, time, physical objects and beliefs would be an example of ontological engineering.[2] Ontology engineering is one of the areas of applied ontology, and can be seen as an application of philosophical ontology. Core ideas and objectives of ontology engineering are also central in conceptual modeling.
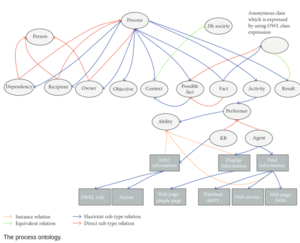
Process ontology (Wikipedia)
In philosophy, a process ontology refers to a universal model of the structure of the world as an ordered wholeness.[1][2] Such ontologies are fundamental ontologies, in contrast to the so-called applied ontologies. Fundamental ontologies do not claim to be accessible to any empirical proof in itself, but to be a structural design pattern, out of which empirical phenomena can be explained and put together consistently. Throughout Western history, the dominating fundamental ontology is the so-called substance theory. However, fundamental process ontologies are becoming more important in recent times, because the progress in the discovery of the foundations of physics spurred the development of a basic concept able to integrate such boundary notions as "energy," "object", and those of the physical dimensions of space and time.
In computer science, a process ontology is a description of the components and their relationships that make up a process. A formal process ontology is an ontology in the knowledge domain of processes. Often such ontologies take advantage of the benefits of an upper ontology. Planning software can be used to perform plan generation based on the formal description of the process and its constraints. Numerous efforts have been made to define a process/planning ontology.[3]
Observational Process Ontology
The Observational Process Ontology (OPO) is a type of ontology that describes the process of observation, specifically in the context of scientific experimentation. It aims to provide a formal, machine-interpretable representation of the steps and conditions involved in making observations, including details such as the instruments and methods used, as well as any relevant background information. OPO is intended to be used as a tool for improving the reproducibility and transparency of scientific research, and can be used in combination with other ontologies to provide a more complete representation of the scientific process.
Scientific Process Ontology
One example of a scientific process ontology is the Scientific Process Ontology (SPO) which is an ontology that describes the different stages and activities involved in the scientific process, such as observation, hypothesis generation, experimentation, and data analysis. The SPO provides a set of classes and properties to represent these concepts and the relationships between them.
Process Ontology
Process Description Ontology
Another example of a scientific process ontology is the Process Description Ontology (ProDO), which is a domain-independent ontology that describes the different stages and activities involved in scientific and technical processes. ProDO provides a set of classes and properties to represent concepts such as processes, inputs, outputs, and agents, and the relationships between them.
Research Object Model
Another example of a scientific process ontology is the Research Object (RO) Model, which is a model for describing the different components and relationships that make up a scientific research object, such as datasets, methods, results, and publications. The RO model provides a set of classes and properties to represent these concepts and the relationships between them. It also includes a set of standards and best practices for creating and sharing research objects, such as the Research Object Bundle (RO-Bundle) format, which is used to package and distribute research objects.
Laboratory Procedure Ontology
Another example of a scientific process ontology is the Laboratory Procedure Ontology (LPO), which is an ontology that describes the different stages and activities involved in laboratory procedures, such as preparing samples, running experiments, and analyzing data. The LPO provides a set of classes and properties to represent these concepts and the relationships between them. It also includes a set of standards and best practices for creating and sharing laboratory procedures.
Experimental Factor Ontology
Another example of a scientific process ontology is the Experimental Factor Ontology (EFO), which is an ontology that describes the different experimental factors and variables used in scientific experiments. It provides a set of classes and properties to represent concepts such as experimental designs, treatments, and measurements, and the relationships between them. EFO also includes a set of standards and best practices for creating and sharing experimental designs and protocols.
The EFO was developed by the European Bioinformatics Institute (EBI) and it's used to support the annotation and integration of experimental data across different domains and applications. It can be used to represent a wide range of experimental factors and variables, from simple protocols to complex multi-step procedures.
The Experimental Factor Ontology (EFO) is an example of a process ontology that focuses on the experimental design and factors used in scientific research. It can be used to represent the experimental design, the materials and the equipment used, and it can also be used to link the experimental data to the results and publications.
Workflow Ontology
Another example of a scientific process ontology is the Workflow Ontology (WfO), which is an ontology that describes the different stages and activities involved in scientific workflows. It provides a set of classes and properties to represent concepts such as tasks, inputs, outputs, and dependencies, and the relationships between them. WfO also includes a set of standards and best practices for creating and sharing scientific workflows.
The WfO was developed by the National Institutes of Health (NIH) and it's used to support the sharing and reuse of scientific workflows across different domains and applications. It can be used to represent a wide range of scientific workflows, from simple protocols to complex multi-step procedures.
The Workflow Ontology (WfO) is an example of a process ontology that focuses on the scientific workflows, which are an essential part of the scientific research process. WfO can be used to represent the procedures, the materials and the equipment used, and it can also be used to link these procedures to the results and publications.
Scientific Method Ontology
Another example of a scientific process ontology is the Scientific Method Ontology (SMO), which is an ontology that describes the different stages and activities involved in the scientific method. It provides a set of classes and properties to represent concepts such as observation, hypothesis generation, experimentation, and data analysis, and the relationships between them. SMO also includes a set of standards and best practices for describing scientific processes.
The SMO was developed by the National Science Foundation (NSF) and it's used to support the sharing and reuse of scientific processes across different domains and applications. It can be used to represent a wide range of scientific processes, from simple protocols to complex multi-step procedures.
The Scientific Method Ontology (SMO) is an example of a process ontology that focuses on the scientific method and its steps and activities
Emulation Framework
There are several ontologies and frameworks that have been proposed to study and understand the concept of emergence in different fields such as philosophy, physics, biology, and computer science.
In philosophy, some theories of emergence propose that emergent properties and phenomena arise from underlying physical or causal processes, such as panpsychism, which proposes that consciousness emerges from physical processes, and supervenience, which proposes that higher-level properties emerge from lower-level properties.
In computer science, ontologies for emergence have been proposed for modeling and understanding the emergence of complex systems, such as multi-agent systems, artificial life, and self-organizing systems. For example, the BDI (Belief-Desire-Intention) model, which is a framework for modeling the behavior of intelligent agents, has been used to study the emergence of group behavior and social phenomena in multi-agent systems.
In the field of complex systems, researchers have proposed different frameworks, such as the Scale-Free network theory, which is an attempt to understand the emergence of complex networks, such as the internet and biological systems. Self-Organization theory, is a framework that seeks to understand how complex structures and behaviors can arise from the interactions of simple agents or components, without the need for central control or explicit design.
In physics, the concept of emergence is related to the emergence of macroscopic properties from microscopic properties, as well as the emergence of new physics and new phenomena at different scales. The framework of Renormalization group theory is often used to study emergence in physics, which is used to understand how physics at small scales relates to physics at large scales.
Epsilon Operator
In mathematics and computer science, epsilon (ε) is a small positive value used as a tolerance or threshold in various contexts. It is often used in numerical analysis to represent the precision of a calculation or the level of accuracy desired. For example, in floating-point arithmetic, it is used to determine the difference between two numbers that are considered equal. In comparison operations, it is used to check if two floating-point numbers are close enough to be considered equal. It is also used in algorithms, such as the epsilon-N algorithm, which is a way to find approximate solutions to problems.
(where "f" upon "x" emerges from "y")
f(x) ε y
(where "y" emerges from "f" upon "x")
Emergence Paths, Circuits & Cycles
Quantum-Framework
1.00 (owl:Class) Є (rdf:Individual) Є
((Reference) Є ( ((Name) Є ( (rdfs:label=Quantum-Framework-Ontology) )
( ((rdf:id=text) = 101) , ((rdf:about)=(RDF) , ((url)=(url)) )
Є ( (Referent) Є (Tensor) Є (owl:Ontology) Є (Individual) Є (Ontology))
0.01 (((Ontology) , (Subject)) , (Complex) =
((Energy) , (Material) , (Machine) , (Habitat) , (Media) , (Trust))
ᑎ ((Activity) , (Action) , (Transaction) , (Reaction))
0.02 ((Ontology) , (Structure=Discipline)) =
((Group=(Arts) , (Group)) = ((History) , (Logics) , (Linguistics) , (Politics) , (Economics) , (Archeology) )),
((Group=(Sciences)),(Group)) = ((Astronomy) , (Biology) , (Chemistry) ,
((Group=(Engineering),Group) = (Computer-Science)) , (Geology) , (Mathematics) , (Physics) ))
0.03 ((Ontology) , (Blueprint)) = User:WikiSysop (This page)
0.04 ((Ontology) , (Complex)) = (Machine)
0.05 ((Ontology) , (Content)) = Computer-Science Logics Computational-Lingustics Mathematics
0.06 ((Ontology) , (Controller)) = ((Notation) Є ((Parser) Є (Content) Є ((Ontology) Є ((Subject) Є ((Discipline))
0.07 ((Ontology) , (Group)) = (Computer-Science)
0.08 ((Ontology) , (Method)) = (Science)
0.09 ((Ontology) , (Model)) = ((Trigger) Є ((Model) Є ((Method),(Blueprint),(Structure)) Є (Controller)) Є (View))
0.10 ((Ontology) , (Notation)) = (MATHML)
0.11 ((Ontology) , (Parser)) = (QbWikiML)
0.12 ((Ontology) , (Place)) = ((Home) ᑌ (Work) ᑌ (Kitchen) ᑌ ((Seminar) Є (School) Є (College))
0.13 ((Ontology) , ((Time)) = (((Near) Є (Here) Є (Far)) ᑎ ((Past) Є (Present) Є (Future) Є (Ever))))
0.14 ((Ontology) , (Trigger)) = ((Range) = (argc Є [(argn=text , argv=text)]) , (not) , (not-me)
0.15 ((Ontology) , (View))(File) = 
Computer-Science-Ontology
1.00 ((Name) Є ( (rdfs:label=Computer-Science-Ontology)
Є ( (Ontology) Є ((Computer-Science-Ontology) = THIS) )
1.01 ((THIS),(Subject)) Є (Markup) Є ( (SGML) Є ((MODCA) , (DSSSL) , (MATHML) , (XSL) , (XSLT))
Є ((HTML) Є ( (XML) , (RDF) , (RDFS) , (SKOS) , (PROV) , (QUBEML)) )
1.02 ((THIS),(Subject)) = ( ((rdfs:Class) Є (CategoryPage)) ᑌ ((rdf:Property) Є (PropertyPage)) ᑌ ((rdf:Individual) Є (MainPage)) )
0.03 ((THIS) , (Blueprint)) = ()
0.04 ((THIS) , (Complex)) = (Machine)
0.05 ((THIS) , (Content)) = ()
0.06 ((THIS) , (Controller)) =()
0.07 ((THIS) , (Group)) = (Computer-Science)
0.08 ((THIS) , (Method)) = ()
0.09 ((THIS) , (Model)) = ()
0.10 ((THIS) , (Notation)) = ()
0.11 ((THIS) , (Parser)) = ()
0.12 ((THIS) , (Place)) = ()
0.13 ((THIS) , (Time)) = ()
0.14 ((THIS) , (Trigger)) = ()
0.15 ((THIS) , (View)) =  ()
()
Computational-Linguistics-Ontology
1.00 (Name) Є (Computational-Linguistics) )
Є ( (Ontology) Є ((Computational-Linguistics-Ontology) = THIS) )
1.01 ((Ontology),(Discipline),(Linguistics))
U (Group = (Applied-Linguistics) ,
(Group = (Computational-Linguistics)) )
1.02 ((THIS),(Subject)) Є (Phonem) = ( (Subject) , (Adjective), (Object) ),
( (Verb) , (Verb-Tense) , (Verb-Modifier) , (Adverb) )
1.03 ((Linguistics),(Subject)) Є (Phenom)) = ( (Measure) , (Unit) , (Scale) , (Modifier) , (Adjective) )
0.03 ((THIS) , (Blueprint)) = ()
0.04 ((THIS) , (Complex)) = (Machine)
0.05 ((THIS) , (Content)) = ()
0.06 ((THIS) , (Controller)) =()
0.07 ((THIS) , (Group)) = (Applied-Linguistics)
0.08 ((THIS) , (Method)) = ()
0.09 ((THIS) , (Model)) = ((Subject) Є ((Content) Є (Sentence) Є (Discourse) Є (Markup))
0.10 ((THIS) , (Notation)) = ()
0.11 ((THIS) , (Parser)) = ()
0.12 ((THIS) , (Place)) = ()
0.13 ((THIS) , (Time)) = ()
0.14 ((THIS) , (Trigger)) = ()
1.01 ((THIS) Є ((Affector) Є (rdf:Property))
Є (Indicative)=(1Є(a)Є 2Є(any)Є 3Є(all)Є 4Є(some)Є 5Є(this)Є 6Є(that))
ᑌ ((Present-Tense)=(1Є(is)Є 2Є(say)Є 3Є(do)Є 4Є(am)Є 5Є(has))
ᑌ (Past-Tense)=(1Є(was)Є 2Є(said)Є 3Є(did)Є 4Є(became)Є 5Є(had))
ᑌ (Future-Tense)=(1Є(will-be)Є 2Є(will-say)Є 3Є(will-do)Є 4Є(will-become)Є 5Є(will-have))
ᑌ (Active-Tense)=(1Є(is:being)Є 2Є(is:saying)Є 3Є(is:doing)Є 4Є(is:becoming)Є 5Є(is:having))
ᑌ (Tense-Modifier)=(1Є(could)Є 2Є(would)Є 3Є(should)Є 4Є(might)Є 5Є(may) 6Є(can))
1.01 ((Linguistics)Є(Axiom))Є (Present-Tense) Є ((Activity) Є (Action)) Є (not))
1.02 ((Linguistics)Є(Axiom))Є (Active-Tense) Є (Present) Є (not)
1.03 ((Linguistics)Є(Axiom))Є (Past-Tense) Є (Past) Є (not)
1.04 ((Linguistics)Є(Axiom))Є (Future-Tense) Є (Future) Є (not)
1.01 ((Linguistics)Є(Axiom))Є (Tense-Modifier) Є (Ever) Є (not)
0.04 (Linguistics),(Method)) Є [(Outline-Parser) , (Label-Parser) , (Inst-Parser) , (Phonem-Parser) , (Phenom-Parser))
Geometry-Ontology
1.00 ((Reference) Є ( ((Name) Є ( (rdfs:label=Geometry) )
Є ( (Ontology) Є (Geometry-Ontology) )
2.01 ((Geometry)Є(Subject))Є ((Arc)ᑌ(Cord)ᑌ(Line)ᑌ(Point)ᑌ(Space)ᑌ(Plane))
2.02 ((Geometry)Є(Subject))ᑌ ((Circle)ᑌ(Ellipse)ᑌ(Arc)ᑌ(Cord)ᑌ(Angle)ᑌ(Gradian))
2.03 ((Geometry)Є(Subject))ᑌ ((Quadrangle)ᑌ(Rectangle)ᑌ(Square))
2.04 ((Geometry)Є(Subject))ᑌ ((Pentagon)ᑌ(Hexagon)ᑌ(Heptagon)ᑌ(Octagon))
2.05 ((Geometry)Є(View))Є ((Graph)Є((LineChart)ᑌ(BarChart)ᑌ(PieChart))
2.06 ((Geometry)Є(Point)Є(Line))Є ((Midpoint)ᑌ(Endpoint)) Є ((Length))
2.10 ((Geometry)Є(3Є(Line))Є(Triangle))Є (Hypotenuse) Є ((Sin) Є (Cos))
2.10 ((Geometry)Є(4Є(Line))Є(Quadrangle))Є (Hypotenuse) Є ((Sin) Є (Cos))
2.08 ((Geometry)Є(Line)Є(Plane))Є ((Width)Є(Area))
2.09 ((Geometry)Є(Plane)Є(Space))Є ((Height)Є(Volume))
0.04 ((Humanities)Є(Subject))Є ((Story)ᑌ(Character)ᑌ(Time)ᑌ(Place)ᑌ(Mood)ᑌ(Theme))Є (Performance)
2.01 ((Algebra)Є(Path))Є (((Origin) Є (Stop)) Є (Path)))
3.01 ((Algebra)Є(Path)Є(Vector))Є ((Origin) Є (Vector))
3.02 ((Algebra)Є(Vector)Є(Matrix))Є (VField)
3.02 ((Algebra)Є(Matrix))Є (VSpace)
3.03 (Algebra)Є(Distance)Є ((Length)ᑌ(Height)ᑌ(Depth))
4.02 ((Physics)Є(Subject))Є ((Tensor)) Є ((Wave) Є (Atom)) Є ((Tensile) Є (Tension))
5.01 ((Biology)Є(Subject))Є (Organism)
5.02 ((Subject)Є(Organism))Є ((Emergence)ᑌ(Emergency)) Є ((Emerging) Є (Emergent) Є (Emerged)
5.02 (Biology)Є(Emergence)Є ((Time)) Є ((Dormancy)Є(Normancy)Є(Urgency)Є(Emergency)Є(Abnormancy))
0.02 ((Subject)Є(View)Є ((Whole)Є(Side)Є((Under)ᑌ(Front)ᑌ(Back)ᑌ(Over)))
((Emergence) Є (Atom)) Є ((System) ᑌ (Complex) ᑌ (Group))
.1 (System) Є (Complex) Є (Group)
.2 (Group) Є ((Group) ᑌ (System) ᑌ (Complex))
(Individual) Є ( ((Structure) ᑌ (Skin) ᑌ (Substrate)) Є ((Machine) Є (Device)) )
(Individual) Є ((Machine) Є (Component) Є (Device))
.1 (Machine) Є ((Wedge) ᑌ (Lever) ᑌ (Incline) ᑌ ((Wheel) Є (Pulley)))
.1 (Machine) Є ((Intake) Є (Supply) Є (Production) Є ((Product) Є (Inventory)) ᑌ (Waste)) Є ((Use) Є (Consumption)) Є (Exhaust))
(Individual) Є (Statement Є ((Subject) ᑌ (Object))) (Individual) Є (Verb) Є (Operation) Є ((Get)Є(Match)Є(Select)) Є (Use) Є ((Consume) ᑌ (Reject))
(Individual) Є ((Noun) Є ((Subject) ᑌ (Object)) Є (((Reference) Є (Referent))
.1 ((Subject) Є (Topic) Є (Academy)) Є ((Tensor) ᑌ (Device) ᑌ (Frequency) ᑌ (Tension))
.2 ((Tensor) ᑌ (Tension) ᑌ (Gradian)) Є ((Device)Є(Machine))
.3 (Subject) Є ((Suppressor) ᑌ (Repressor) ᑌ (Expressor) ᑌ (Depressor))
.4 Tensor Є ((Organism)ᑌ(Specimen)) Є (Population) Є (Genus) Є (Class) Є (Phylum) Є (Domain) Є (Kingdom) Є (Realm))
.5 (Tension) Є (Frequency)
.6 (Gradian) Є ((Notation) ᑌ (Unit) ᑌ (Measure) ᑌ (Scale))
(Individual) Є (Academy) Є "Agronomies" ᑌ "Archeologies" ᑌ "Astronomies" ᑌ "Biologies" ᑌ "Economics" ᑌ "Mathematics" ᑌ "Physics" ᑌ "Sociologies"
(Individual) Є rdfs:Class Є ((Reference) ᑌ (Referent) ᑌ (Gradian))
.5 rdfs:Class Є ((Title)ᑌ(Name)ᑌ(Identifier)) Є rdfs:Label
.6 rdfs:Label Є ((Vocabulary) Є (Taxonomy) Є (Catalog) Є (Thesaurus) Є (Encyclopedia) Є (Wiki) )
.9 ((Reference) Є ((Node)ᑌ(Anode)ᑌ(Triple)))
(Verb) Є ((should-be)ᑌ(could-be)ᑌ(would-be)ᑌ(may-be)ᑌ(will-be)) Є (can-be) Є (must-be))? Є (being)? Є (is) Є (was) Є (been)
.1 (Being) Є (Actor) Є (Speaker) Є (Doer) Є (Auditor) ((Speech)ᑌ(Gesture)ᑌ(Motion)Є(Scripted)) Є (Acted) Є (Completed)
.1 (Actor) Є (Activity) Є (Acting) Є (Action) Є ((Speech)ᑌ(Gesture)ᑌ(Motion)Є(Scripted)) Є (Acted) Є (Completed)
.2 ((Speaker) Є (Actor)) Є ((Saying)Є((Narrating)Є(Story))) Є (Say) Є ((Said) Є (Storied)) Є (Finished)
.2 ((Doer) Є (Actor)) Є (((Saying)Є(Doing))Є(Performing)Є(Becoming)) Є ((Performance)) Є ((Say)Є(Do)Є(Perform)Є(Become)) Є ((Performed)Є(Said)Є(Done)) Є (Became)
.2 ((Doer) Є (Actor)) Є (((Saying)Є(Doing))Є(Performing)Є(Becoming)) Є ((Performance)) Є ((Say)Є(Do)Є(Perform)Є(Become)) Є ((Performed)Є(Said)Є(Done)) Є (Became)
.3 ((Seer) Є (Actor)) Є ((Seeing)Є(Looking)Є(Staring)) Є ((See)Є(Look)Є(Stare)) Є ((Looked)Є(Stared)) Є (Saw)
.4 (Auditor) Є ((Hearing)Є(Considering)Є(Analysing)Є(Learning)) Є ((Consideration)Є(Analysis)Є(Learn)) Є ((Considered)Є(Analysed)Є(Learned)) Є (Heard)
.5 (Mover) Є ((Leaning)Є(Falling)Є(Moving)) Є ((Lean)Є(Fall)Є(Movement)) Є ((Leaned)Є(Fallen)) Є (Moved)
(Individual) Є (Modifier) Є ((Adjective) ᑌ (Adverb) ᑌ (Participle)
- CockroachDB
- Towards an emulation tool based on ontologies and data life cycles for studying smart buildings
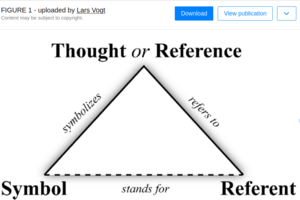
Referents and References
In semantics and philosophy, a referent is used to establish a connection between a word, phrase, or symbol, and the thing or object it represents or denotes. This allows for clear communication and understanding of the meaning of language. In programming, referent is not commonly used, but it can be used in similar way to establish a connection between a variable or identifier and the object it references.
This epistemology claims all ontologies must first distinguish their expressions as being references to things that exist, or as the things that exist themselves. All ontologies must define "Referent" and "Reference" as top-level classes of expression otherwise persistent semantic confusion risks the support of a user base that cannot perceive any fundamental organization of the ontology.
Implication. Because language, symbols and numbers are used to name things, any Name, Symbol or Identifier is a reference to the concept being described. Referents thus emerge from References, and Referents are thus preceded by instantiation of its Reference. A principle of Emergence applies in this manner: A Reference may exist in Time without a Referent, emerging subsequent as "completed" once the Referent is associated with its Reference. Alternatively, a Reference has not emerged and is "Incomplete", until its association with a Referent.
Implication. Because Referents may be maintained in or referenced by a Catalog classified per a Referent Class, ontologies are required to support these axioms and forms.
1.1 Reference Є Referent Є Catalog
1.2 Reference Є Referent Є Catalog_Reference Є Catalog
1.3 Catalog Э Referent Э Reference
1.4 Catalog Є Referent Э Reference
In 1.1, a specific process for instantiation is indicated for any particular Referent: a particular Reference is instantiated and a non-specific Catalog is thereafter instantiated. A Reference_Catalog is distinguished from a Referent_Catalog by its structure, that is, whether the Catalog contains References or contains Referents; in the latter case, one would expect the Catalog to be a database or serialized data-set, e.g., a Shelf of Books, while all Referent "indexes" are perforce Reference Catalogs, e.g., a each Catalog entry is a References to some individual, set or group of Books.
In 1.2, a specific Catalog is to be created for any Referent_Class
The following material is being rewritten
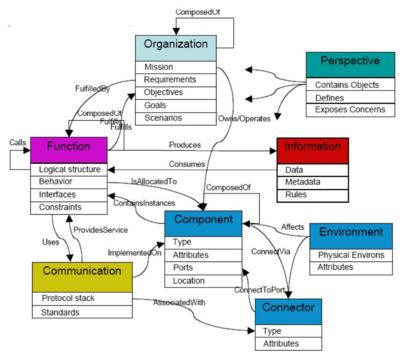
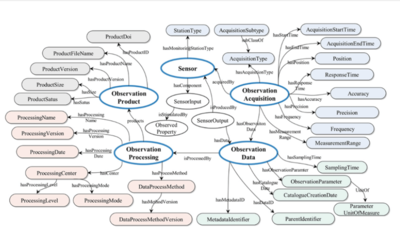
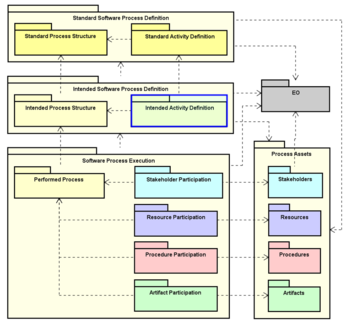
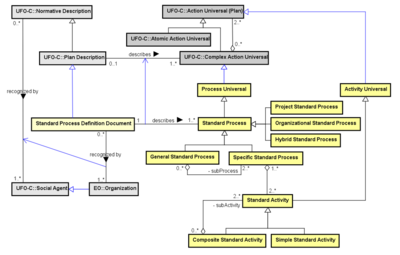
The Best Practices Wiki Information Model is fundamental to identify (a) semantic tags to markup Best Practices essays (b) semantic classes for Practice, Policy, Procedure and Process models, of prime interest (c) classes for Act, Action, Activity and Task that are the detailed enumerated steps for a "method" that achieves a particularly useful objective.
Related Open Source
mw:Extension:SemanticTasks: provides email task notifications and reminders whose model is centered on assignment of Users to Tasks.
References
- [https:\\kissflow.com/workflow/bpm/business-process/ The Extensive Guide to Business Processes]
- ERP Readiness Series: The Four Core Processes Every Business Should Document
Referents
Partitive Classes
Taxonomic Classes
Topic Annotation (Tags)
Linguistic Classes
Instance Referents
{{Category:Tag <br/>|rdfs:subclassOf=Reference <br/>|name= <br/>|id= <br/>|label= <br/>|path= <br/>|timestamp= <br/>|@category:name }} <!-- {{Hierarchy|Start|2|skos:Concept|https://www.w3.org/2004/02/skos/}} {{Hierarchy|End|2|Gender|skos:Concept}} -->
Determiners include articles (a, an, the), cardinal numbers (one, two, three...) and ordinal numbers (first, second, third...), demonstratives (this, that, these, those), partitives (some of, piece of, and others), quantifiers (most, all, and others), difference words (other, another), and possessive determiners (my, your, his, her, its, our, their).
Best Practices Wiki Ontology
- upgrade to https
- Done upgrade skin install site logo icon and thumbnails
- re-install previous path and related configs
- upgrade replace or drop previous extensions
- clean up directories and update documentation
- add user-form to specify images for an SEO category
- identify articles not listed by Best Practices List by Category
- near term - add articles about IT practices
How to create a new articleCreate a new page title somewhere -- that's the key. Whenever you see a red page title So, how do you "create a new page title somewhere"? You can Just add That's all there's to it. |
How to upload a file or imageCreate a new image title somewhere -- that's the key. Whenever you see a red image title So, how do you "create a new image title somewhere"?
That's all there's to it. |