User:WikiSysop/Information Model
The Best Practices Wiki Ontology
An Emergence Epistemology for Modern Ontologies
On the heels of recent evolution in mathematics and astronomy, physics, biology, social sciences, and cognitive research, a new approach to the process of information modeling is needed to support widely common cross-domain requirements, that is, this article proposes a candidate Standard Ontology Model (SOM).
Motivation
Presently ontologies are built using approaches first typified by the Formula Translating System (FORTRAN), and are thus based on essential notions of "data structures" as proxies for operands to an algebraic formula; "routines" being a particular functional formula; and "return values" being the specific knowable output of the formula. The generic formula, y = f(x) (where "y" is equal to "f" upon "x") exactly maps to the widespread Input-Process-Output model underpinning many methods; it is aptly descriptive to consider the Algebraic Formula the epistemology used to fashion many ontologies.
However if success of ontologies is judged by their fruits, the Formula paradigm appears to have produced representations of reality that are not being used to any depth, by anyone, for the principle reason the ontologies being promulgated have no bearing upon the actual models being developed, and tested, by a data scientist most concerned with theories of interaction and evolution within their domains. The core problem is no public domain ontology exists to structure problem-solving by data scientists, thereby reducing use of ontologies to that of an important public service.
Formulaic data structures first emerged as Database Systems and then as Triple Stores. Triple Stores consolidated gargantuan systems of DBMS tables, using ontologies as a dictionary of existential relations between keys inherited from those tables, in hopes of reducing processing costs while increasing processing opportunities.
The Resource Description Framework (RDF) introduced a model for an "Axiom" (expressed in an RDF Notation) with its rdf:Statement, a "triple" composed of {rdf:Subject, rdf:Predicate, rdf:Object} and essential to logic formulas. The RDF sought to accommodate its rival meta-model by publishing a standard for rdf:Pair = {rdf:First, rdf:Rest}. Meanwhile the Standard Model for computer science students was made to be a triple relation too, Model-View-Controller, to cater to the growing orientation towards database models, process models and ontology models.
(where "f" upon "x" emerges from "y")
f(x) ε y
(where "y" emerges from "f" upon "x")
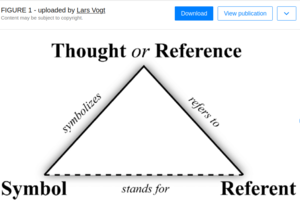
Referents and References
In semantics and philosophy, a referent is used to establish a connection between a word, phrase, or symbol, and the thing or object it represents or denotes. This allows for clear communication and understanding of the meaning of language. In programming, referent is not commonly used, but it can be used in similar way to establish a connection between a variable or identifier and the object it references.
This epistemology claims all ontologies must first distinguish their expressions as being references to things that exist, or as the things that exist themselves. All ontologies must define "Referent" and "Reference" as top-level classes of expression otherwise persistent semantic confusion risks the support of a user base that cannot perceive any fundamental organization of the ontology.
Implication. Because language, symbols and numbers are used to name things, any Name, Symbol or Identifier is a reference to the concept being described. Referents thus emerge from References, and Referents are thus preceded by instantiation of its Reference. A principle of Emergence applies in this manner: A Reference may exist in Time without a Referent, emerging subsequent as "completed" once the Referent is associated with its Reference. Alternatively, a Reference has not emerged and is "Incomplete", until its association with a Referent.
Implication. Because Referents may be maintained in or referenced by a Catalog classified per a Referent Class, ontologies are required to support these axioms and forms.
1.1 Reference Є Referent Є Catalog
1.2 Reference Є Referent Є Catalog_Reference Є Catalog
1.3 Catalog Э Referent Э Reference
1.4 Catalog Є Referent Э Reference
In 1.1, a specific process for instantiation is indicated for any particular Referent: a particular Reference is instantiated and a non-specific Catalog is thereafter instantiated. A Reference_Catalog is distinguished from a Referent_Catalog by its structure, that is, whether the Catalog contains References or contains Referents; in the latter case, one would expect the Catalog to be a database or serialized data-set, e.g., a Shelf of Books, while all Referent "indexes" are perforce Reference Catalogs, e.g., a each Catalog entry is a References to some individual, set or group of Books.
In 1.2, a specific Catalog is to be created for any Referent_Class
The following material is being rewritten
The Best Practices Wiki Information Model is fundamental to identify (a) semantic tags to markup Best Practices essays (b) semantic classes for Practice, Policy, Procedure and Process models, of prime interest (c) classes for Act, Action, Activity and Task that are the detailed enumerated steps for a "method" that achieves a particularly useful objective.
Related Open Source
mw:Extension:SemanticTasks: provides email task notifications and reminders whose model is centered on assignment of Users to Tasks.
References
- [https:\\kissflow.com/workflow/bpm/business-process/ The Extensive Guide to Business Processes]
- ERP Readiness Series: The Four Core Processes Every Business Should Document
Referents
Partitive Classes
Taxonomic Classes
Topic Annotation (Tags)
Linguistic Classes
Instance Referents
{{Category:Tag <br/>|rdfs:subclassOf=Reference <br/>|name= <br/>|id= <br/>|label= <br/>|path= <br/>|timestamp= <br/>|@category:name }} <!-- {{Hierarchy|Start|2|skos:Concept|https://www.w3.org/2004/02/skos/}} {{Hierarchy|End|2|Gender|skos:Concept}} -->
Determiners include articles (a, an, the), cardinal numbers (one, two, three...) and ordinal numbers (first, second, third...), demonstratives (this, that, these, those), partitives (some of, piece of, and others), quantifiers (most, all, and others), difference words (other, another), and possessive determiners (my, your, his, her, its, our, their).